Huum...long time since my last writing about Japan Earthquake. Now I'm back with akin of astronomical writing! Hahaha it has been long since my last contact with astronomy. Let me count, umm it has been 1 year!
Now I will write about Saros Cycle. Saros cycle is one of eclipse cycle used by most astronomer, because of its famous pattern. Saros cycle is derived from 3 known variables: the synodic month, which is the time taken by moon from a new moon to another new moon (29.530589 days; this also being the base for Islamic Month), anomalistic month, the time take by moon from perigee to another perigee, it is 27.554550 days (perigee is the point where moon is in the closest position to the earth), and the draconic month, the time take by moon to move from one node to another node, it is about 27,212221 days. A node is a crossing made by the coincidence of lunar orbit and the ecliptic.
The Saros cycle is an eclipse cycle consisting 6585.322 days or 6585 days + 7 hours + 43 minutes + 40.8 seconds. That means, if at June 15, 2011 at 20:13 UT there will be total lunar eclipse with center of visibility at Indian Ocean, there should be another total lunar eclipse at June 25, 2029 at approximately 27:56 UT (or June 26, 2029 at approximately 03:56 UT) with the center of visibility 7 hours + 43 minutes + 40.8 seconds (or 115 degrees, 55 minutes, 12 seconds) farther west: South America region. That two lunar eclipses are in one Saros cycle. This Saros cycle is also applied for Solar eclipses, but its calculation for its precise hour and location are more difficult than that of lunar eclipse.
The more rarely used Exeligmos cycle comprises of 3 Saros cycles to compensate the .3 residue of the Saros. Its advantage is, the longitude of predicted lunar/solar eclipse will not differ much than the previous 54 years-ago eclipse. But until today, astronomers still prefer Saros to Exeligmos cycle.
A Saros serial is a serial of eclipses occur in consecutive Saros cycles, and each serial should be numbered. Saros serial have a start and an end, because the two nodes are moving westward. In each Saros cycle, the nodes move 0.4779 degrees in 2000 to 3000; that value is changing significantly each millenia. The start of a Saros cycle is marked by the presence of penumbral lunar eclipse or partial solar eclipse in the polar region. Each time the Saros cycle completed, the eclipse becomes darker, the totality becomes longer. Then the Saros serial reached its maxima; the node is directly overhead in equatorial region. After that, the Saros serial will run into its terminus; the totality becomes shorter, and it ended with penumbral lunar eclipse or partial solar eclipse, in the opposing Earth's pole.
The Calculation of Lunar Eclipse Based on Saros Cycle
Example: take an eclipse, say it is June 15, 2011 eclipse. From above explanation, we know that another eclipse occur with the same Saros serial will be at June 25, 2029 (from the addition of June 15, 2011 with 6585 days; you can do it in Microsoft Excel with ease).
Now we want to know the time:
The June 15, 2011 eclipse will be peaked at 20:12:36 UTC. The June 25, 2029 total lunar eclipse will be peaked at (20:12:36 + 7:43:40) = 27:55:40
nah, because there is no 27 o'clock, we should convert it to more rational form: 1 day + 03:55:40 UTC. So now the date and time of eclipse is June 25, 2029 + 1 day + 03:55:40 = June 26, 2029 at 03:55:40.This is only a rough estimation for the time, because we don't count the effect of tidal forces between sun, earth, and moon, the effect from nutation of moon, radius of earth and earth's atmospheric aberration. But remember that our calculation from Saros cycle alone is accurate to the hour.
For the location, each lunar eclipse separated by 1 Saros cycle will move 115 degrees, 55 minutes, 12 seconds farther west. This June 15, 2011 eclipse will be visible throughout East Asia, India, Australia. After one Saros cycle or at June 26, 2029, the central of visibility of total lunar eclipse will move to South America, Antarctica, West Africa. Then after one Saros cycle, or total lunar eclipse of July 7, 2047, the central of visibility will be Pacific Ocean and Australia, and so on.
For the kind of lunar eclipse that would be happen, we can use the standard regression of node every Saros cycle: 0,4779 degrees each cycle. Taking June 15, 2011 total lunar eclipse which node is located after the umbral center, and the umbra which is about 2000 km wide (and the revolution of earth made the time taken by umbra to cover the moon will be slightly longer), we can predict that total eclipses for this saros serial still persist well slight after 2100.
For the location, each lunar eclipse separated by 1 Saros cycle will move 115 degrees, 55 minutes, 12 seconds farther west. This June 15, 2011 eclipse will be visible throughout East Asia, India, Australia. After one Saros cycle or at June 26, 2029, the central of visibility of total lunar eclipse will move to South America, Antarctica, West Africa. Then after one Saros cycle, or total lunar eclipse of July 7, 2047, the central of visibility will be Pacific Ocean and Australia, and so on.
For the kind of lunar eclipse that would be happen, we can use the standard regression of node every Saros cycle: 0,4779 degrees each cycle. Taking June 15, 2011 total lunar eclipse which node is located after the umbral center, and the umbra which is about 2000 km wide (and the revolution of earth made the time taken by umbra to cover the moon will be slightly longer), we can predict that total eclipses for this saros serial still persist well slight after 2100.
Beside the time, location, and kind of eclipse, we should also know the number of Saros serial of the eclipse. For July 15, 2011 total lunar eclipse, the number of Saros serial is 130, and so does with the July 26, 2029 eclipse and so on. 130 is an even number. Even number representing that the eclipse occurs at moon's ascending node. The last penumbral eclipse of this series will put the moon left of the earth's umbra, if our view to west. The opposite happen with odd Saros serial number (see figure below, the first eclipse of the odd Saros serial is located below the image, or left side of earth's shadow if our view is to west. Moon is at descending node).
The Calculation of Solar Eclipse
While the calculation of Lunar eclipse is easier because of we doesn't take much concern on location, the calculation of Solar eclipses is far more complicated, because, besides of determining the location, we should also determine how far is the moon from the earth. The distance of moon from the earth constitutes the kind of eclipse whether it is partial, hybrid, or annular. Much of this calculation has been taken by supercomputers. By means of Saros cycle, we could only determine the date, and rough time in UTC.
There are some patterns appear on solar eclipses:
1.) Two solar eclipses split by 354/355 days are separated by 10 saros series, example: The June 21, 2001 total solar eclipse of Saros 127 in Atlantic and South Africa and the June 10, 2002 Annular solar eclipse of Saros 147 in Mid-Pacific. But this pattern is limited: only 4 - 6 eclipses can match this pattern every 16-18 normal year - because this pattern is derived from Islamic calendar. In Islamic calendar, there are 12 cycles, based on the amount of Islamic months every year.
I give you the description of Islamic calendar eclipse pattern below.
I give you the 29-Muharram solar eclipse cycle. This means that an eclipse will occur always at 29 Muharram in a certain year. Consider if the cycle starts at Islamic year 1300 - this means, prior to 1300 there is (considered) no (recorded) solar eclipses at 29-Muharram. It will stop at about the Islamic year 1306 - this is the year when solar eclipses stopped to occur at 29-Muharram, and starts to occur at 29-Muharram again at 1300 + 22 years = Islamic year 1322. An Islamic calendar is consisting of 354/355 days, while the normal year is 365/366 days.
2.) Two solar eclipses split by 1 Inex or 10571.95 days ( about 29 years minus 20 days ) are in consecutive Saros series. Example: The June 21, 2001 total solar eclipse of Saros 127 in Atlantic and South Africa and June 01, 2030 annular solar eclipse in Russia with Saros number 128. This is the base theory for making the Saros-Inex Panorama, a diagram that consisting the date thousands of solar eclipses as appeared below.
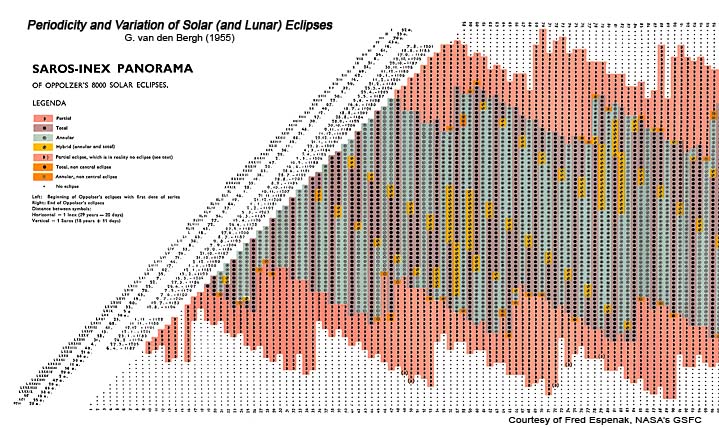
3.) Normally, each move of 1 Saros cycle will put the center of solar eclipse more northwest than its previous location. This is due to difference between Synodical Saros cycle and Draconical Saros cycle as many as 0.036 day.4.) But, the date when it fall can cause an anomaly for the point 3.) statement. This anomaly can cause the Saros serial "doesn't work as usual": The path of solar eclipse can be still located at equatorial region with total eclipse occur in a consecutive Saros cycle like this example:
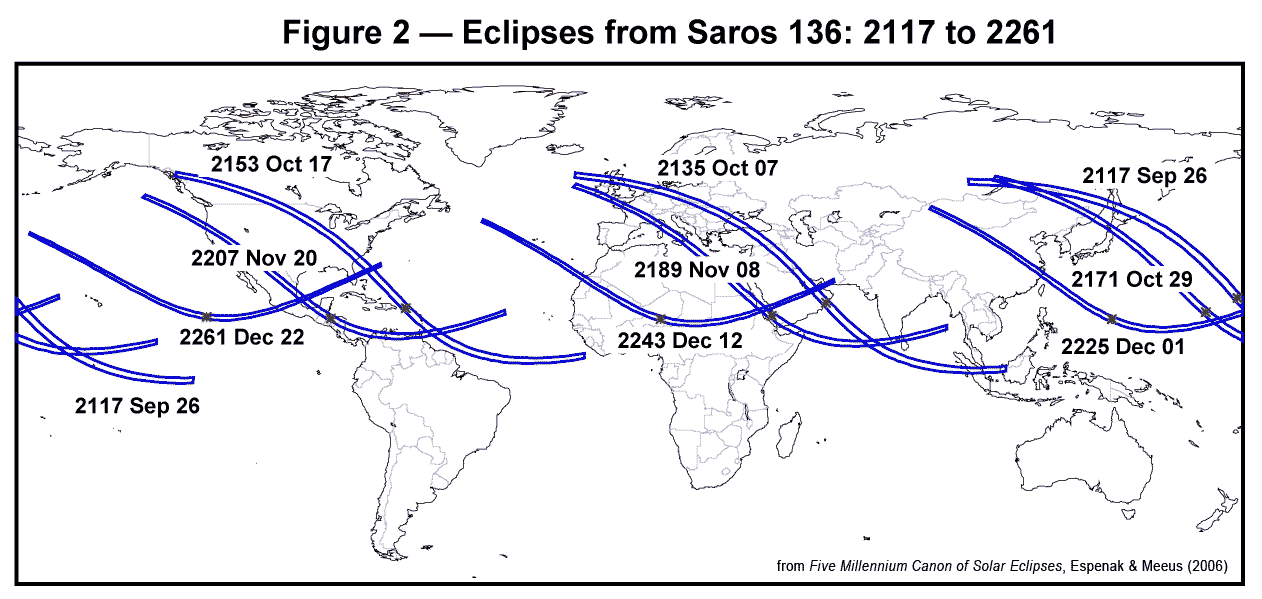
The example above is an anomaly of Saros cycle because that nine Saros serial 136 solar eclipses are falling in coincidence with southern summer, so the northern part of earth is tilted away faster than the change of moon's inclination.In solar eclipse, there are more variables constituting the type, place and specific hour (not date), since it affects only a small area and very short period of time. The variables are gamma (the distance of the apex of moon's shadow to the center of earth divided by the radius of earth), delta T (the difference between UTC and Terrestrial time), and Besseliant Elements (an arranged values to calculate and predict the local circumstances of eclipse for an observer on Earth).
