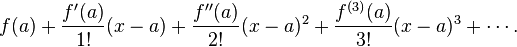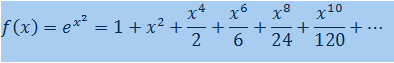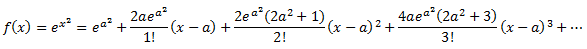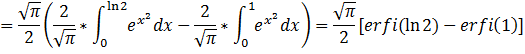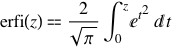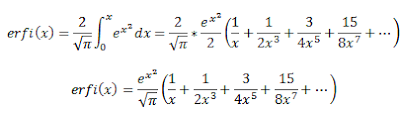Sorry I'm trashing here with math. Actually, it was a problem given during a university admission test. A Math problem, actually university semester II Calculus. Why I should say sick? It wasn't attested in Big-Three Indonesian university; Bandung Tech Institute, dubbed to be the best technological university in Indonesia didn't give the problem at its admission test (Bandung Tech always give some mind tricking problems, in which an excelled student can do it fast by finding the patterns), neither did my Gadjah Mada nor University of Indonesia.
This problem came from a university in Semarang: Diponegoro University.
The problem is like this:
Seems easy at a glance. But it is actually harder. We should integrate it from the inner part dx then we do the outer part dy.
Seems easy at a glance. But it is actually harder. We should integrate it from the inner part dx then we do the outer part dy.
which is equal to:
After that, we integrate the outer part,
becoming
This second part is the hardest part
2. Integrating the ey2 is not as easy as I thought. After dealing with u=y2 form, the equation goes ill by the form 2×√u which is adding up to infinity if we try to integrate it by multiple integral method (and I will talk about this later). It is known that the function f(y)= ey2 is an even function, a function in which f(-y)=f(y). But the problem is, the function's value goes ∞ when x approaches ∞; so the simplest thing we can do when integrating ey2 is integrate it by mean of series. A function f(x) could be approached approximately with an infinite series:
2. Integrating the ey2 is not as easy as I thought. After dealing with u=y2 form, the equation goes ill by the form 2×√u which is adding up to infinity if we try to integrate it by multiple integral method (and I will talk about this later). It is known that the function f(y)= ey2 is an even function, a function in which f(-y)=f(y). But the problem is, the function's value goes ∞ when x approaches ∞; so the simplest thing we can do when integrating ey2 is integrate it by mean of series. A function f(x) could be approached approximately with an infinite series:
Nah, you can replace a with any real number. Usually, scholars use the number 0 for simplicity, and putting 0 as a will make the series called MacLaurin Series.
Now we replace the y in f(y)= ey2 into x and the function becomes f(x)=ex2. The infinite series for f(x) when a =0 becomes:
If you prefer to put another real number as a, then this equation could be used.
Getting that kind of equation, we could easily integrate the f(x)=ex2 by integrating its series expansion.
But in this article i prefer not to do the exponential integration that way.
Why not? Because the xn in the series expansion grows significantly smaller than the exponential function. I'm intending to give a more precise result using error function. I will do the error function with the touch of series expansion also; but if i do with the error function, the result will precise up to 10-5 order.
But in this article i prefer not to do the exponential integration that way.
Why not? Because the xn in the series expansion grows significantly smaller than the exponential function. I'm intending to give a more precise result using error function. I will do the error function with the touch of series expansion also; but if i do with the error function, the result will precise up to 10-5 order.
ERROR FUNCTION
So what another silly thing you would suck on my head?
OK readers, take a break please. Yeah now I want to give you an important function, it is error function. Built on the basis of Gaussian integral, the error function was firstly used only at statistical data processing. Now this function is used also in advanced physics, thus this function is given as early as one or two year after Indonesians entering science faculties in university. I will only give you some basics of error function relating to the sick math problem above.
Go back to the exponent integral, we could further analyze the integral like below. Note that the ey2 is replaced by ex2.
OK readers, take a break please. Yeah now I want to give you an important function, it is error function. Built on the basis of Gaussian integral, the error function was firstly used only at statistical data processing. Now this function is used also in advanced physics, thus this function is given as early as one or two year after Indonesians entering science faculties in university. I will only give you some basics of error function relating to the sick math problem above.
Go back to the exponent integral, we could further analyze the integral like below. Note that the ey2 is replaced by ex2.
Then,
This is it. The erfi(z) function is defined by:
And so, its MacLaurin series is
Erfi(z) or erfi(x) series when x=∞ is calculated by integrating the ex2 dx endlessly.
The picture below give an image on how to do it.
so, the erfi(x) becomes:
That are two kinds of series expansion for erfi function. We should use the erfi MacLaurin series when calculating figures less than 1 or more than -1. The erfi series expansion at x=∞ is used when calculating figures more than 1 or less than -1. If the figure is 1, you can use either the infinite or MacLaurin series.
Then, we do the erfi(ln 2) - erfi(1) by means of series expansion. We do them by mean of erfi MacLaurin series, this yields -0.72270466, just differ 2 x 10-8 with the result yielded by a math software.
Next, the final result is:
The term 0.02677468 can be rounded to be 0.0267747 which differs 8 x 10-9 with computer's computation result.
